上了一學期的資訊隱藏
從第一堂課開始介紹資訊隱藏(藏匿學)與密碼學
了解藏匿學和密碼學兩者的相似與相異之處,兩者的訴求不同。
剛好我這學期 上數位簽章牽涉到很多加解密的方法,
而資訊隱藏這門課剛好互補,是屬於藏匿學的部份
這堂課的要求是多參予討論,上完課後到BLOG留個紀錄
我喜歡小班制這樣的上課模式,上課可以問問題。
我認為台灣的學生,對於問問題實在是感覺到非常恐懼
有害羞的,也有不懂裝懂的,大家都還不習慣這種上課方式
因為從高中開始就是這樣填壓式的學習,
高中老師說什麼就是什麼,問問題,老師也不見得回答你
他反而要求你要自己回家多看書。
我認為興趣很重要,我在高中的時候,對英文最有興趣
有很大的部份是因為我喜歡那個老師上課的方式,
他跟我說: 人的心本來就是偏的,你若偏心英文,英文就會偏心你。
我聽說一年級的歷史課,有位老師鼓勵學生多問問題,多發表意見
那位歷史老師說,只要舉手亂發表建議,回答問題不論對錯,
都可以拿獎金壹百元 ,課後留下一些時間讓同學上台,隨便講任何事情,
說笑話也好,談自己的生活也好,只要上台發表就有獎金
聽說他們上課的舉手風氣很熱絡。
我聽到學弟在述說這件事情的時候,覺得這位教授很有遠見,
因為他抓到台灣教育最大的核心問題,學生不懂不問,又愛裝懂。
雖然上一門的課,他所花的cost比較高一點,
藉由這種手段,也許達到他要的效果與目的。
而資訊隱藏這門課,希望用討論的方式來上課,我覺得出發點很好,
但是我認為討論的還是太少,應該要去想一個好的方式讓學生參予更多,
另外一方面是學生自己太害羞也是個問題。
我覺得資工系要好,應該要先從讓學生舉手,主動式學習開始,
從一年級就要開始。
被動式學習是教授給什麼就接受什麼,全面吸收,這樣比較不好。
我一年級進資工,覺得超沒有興趣的,教授一開口,滿嘴英文
對於電腦白癡的我,真的是鴨子聽雷
我覺得"沒有興趣"和"不曉得資工在幹麻" 是一年級最大的問題
所以我認為教授引導學生產生興趣很重要,還有鼓勵舉手這件事
對我來說啟蒙最大的是顏老師,他經常鼓勵我不要怕,盡量舉手
不管說對說錯,都加分,因為舉手就是一種勇氣
我今年有修軍訓課,軍訓老師也希望有互動,但是還是沒有互動
為什麼?
我覺得台灣的學生太害羞,當你給他們機會舉手發問的時候,
大多都不敢舉手,還有在意別人的眼光,怕別人覺得自己很笨
請給他們一些時間,讓他們能和自己心中的阻礙抗衡
大多的學生都還在猶豫要不要舉手的時候
教官已經跳開到另外一個話題了
不要期盼所有的學生都舉手,像所有的研究一樣
我們講的不是百分之百的效能,我們講究的是"提升了多少效能"
從0個人舉手,到五六個人舉手問問題,參予討論,這就是提升的部份
從LSB 到Index Embedded,講究的並不是毫無破綻的藏匿
講究的是 How much you can improve ?
這句話,算是我上課我受益良多的一句話。
回到正題,這學期學了兩種資訊隱藏的方法,接下來還要學第三種
一種是LSB 一種是Index Embedded,這兩種都是用於調色盤 based 的藏匿方式
之後還要學習 JPEG 的藏匿方法。
在藏匿學的課中,除了思考藏的方式,也去想破解的方式。
還有討論如何去判斷圖是否為一張亂亂的影像。要大家去思考。
之後看了一篇論文,這篇論文是我在大學第一篇關於多媒體領域的論文
然後教授要我們看這篇論文提出問題,
不管多簡單的問題都可以問,包括英文單字也可以問。
然後要我們做投影片報告這篇論文,然後指出作報告時的優缺點,
我喜歡這樣的上課方式,下次若有類似的課程,
我希望多發幾篇論文給學生看,做小組分工
然後上台報告的人接受底下的人問問題,是問問題、給意見而不是批判(評)
最好高年級跟低年級穿插在同一組
因為這樣學弟妹可以直接從學長姐身上學到作投影片的經驗,還有報告的經驗
這樣會更像做研究。
因為我覺得研究就是 抓住別人的缺點,掌握自己的優點
然後改善別人的缺點,增強自己的優點
我現在開始跟教授作研究了,我們報告的時候,教授和學長姐在下面問問題
我深覺一件事情: 教授也不是萬能的,他們也會問問題,他們也有問題
教授都有問題了,作為學生的,問問題的風氣和能力不應該比教授還要差
顏老師跟我說: 等你唸到博士碩士,已經不是老師交你了,而是反過來
你要去交老師,老師只給你一些方向和建議
這門課,教授在課堂上給我們看過一個影片 -- 地球是平的
那個影片的確也shock到我了,我大學所學的東西,
說實在的,在沒有複習的情況下,忘的一乾二淨,不記得學了些什麼
像影片所說的,只有不變的東西留下來-- 態度
我記得有一次上課,是要拿自己改進的投影片上台,
我想說我的投影片只有兩頁,實在是沒有什麼好改進的,
但是看到教授的投影片後,他說他改了一個禮拜,
圖都重新畫,我心中OS: 教授怎麼比學生還認真!!
這件事情給了我一個觀念,投影片要精心策劃,每一張投影片都要有功能
報告的時候要抓重點,怎麼抓重點需要學習
所以在未來研究所的課程裡,我立志論文中的圖能重畫盡量重畫
因為會比較清楚,而且可以加入動畫
以前有一個英文老師對我說: 上台就是一種表演,表演是一種藝術
而我認為,若上台報告是種表演,
在舞台上Focus住觀眾,也就是Focus住了Money
甚至讓觀眾很期待你的下一次表演。
這學期的資訊隱藏課程,上課方式我很喜歡,
我的優點是上課積極參與討論,經常私下和本泰可欣討論
出席狀況良好,沒有遲到過,BLOG 的篇數還可以
缺點是BLOG寫的不夠豐富,沒有寫程式,有一兩次缺席
對於課程內容了解與滿意,清楚課程目標
我給自己的分數是 70 分。
2007年6月19日 星期二
2007年6月13日 星期三
Week 9 : Paper 心得
這個禮拜,我們看一篇Paper,並寫下心得。
我的第一個問題是: 如果closest color很多,但是卻剛好沒有parity
這種情況是有可能會發生的。
第二種情況剛好相反,Parity很多,但是都是不相似的顏色
這種情況也是有可能發生的。
第三個問題是,兩種不同顏色,是否有可能會有同一組closest color且parity 一樣
經過老師講解後,第一個問題始有可能會發生,但是機率很小。
第二種情況也有可能會發生。重點不是(R+G+B)mod 2這個公式
事實上我們也可以用別的公式來產生Parity,
但是我們希望找顏色最接近的來當Parity
第三個問題,答案是會有這種情況的。
我的第一個問題是: 如果closest color很多,但是卻剛好沒有parity
這種情況是有可能會發生的。
第二種情況剛好相反,Parity很多,但是都是不相似的顏色
這種情況也是有可能發生的。
第三個問題是,兩種不同顏色,是否有可能會有同一組closest color且parity 一樣
經過老師講解後,第一個問題始有可能會發生,但是機率很小。
第二種情況也有可能會發生。重點不是(R+G+B)mod 2這個公式
事實上我們也可以用別的公式來產生Parity,
但是我們希望找顏色最接近的來當Parity
第三個問題,答案是會有這種情況的。
week13: PPT Design (2)
今天上課的目的,要我們把上次的PPT經過修改
再Present一次,我的雖然有改,但是我卻不太想上台
因為我覺得實在是沒有什麼好講的
我的投影片只有兩頁,我只有把版面稍微調的漂亮一點而已
因為我已經做的很精簡了,再精簡可能沒辦法了。
只能往別的地方發展。
投影片放在網路硬碟上: webhd.mcu.edu.tw
分享名稱: IMH Class
雖然當初會有這樣的想法,但是看到老師修改的投影片後
覺得自己有點弱了
蓮老師都那麼認真的再作投影片,我怎麼能鬆懈呢?
而且又製作動畫,加上所有的圖都自己重新再畫。
我最近也開始要報告了,我看到我學長他們做的投影片
和老師做的投影片,比較起來,真的可以看的出來有沒有用心在報告
後來我做投影片開始把圖重新畫,加上動畫
一篇論文有很多東西,在三小時內,我應該要報告哪些東西,
我覺得這是一件困難的事情,是我還需要去學習的。
再Present一次,我的雖然有改,但是我卻不太想上台
因為我覺得實在是沒有什麼好講的
我的投影片只有兩頁,我只有把版面稍微調的漂亮一點而已
因為我已經做的很精簡了,再精簡可能沒辦法了。
只能往別的地方發展。
投影片放在網路硬碟上: webhd.mcu.edu.tw
分享名稱: IMH Class
雖然當初會有這樣的想法,但是看到老師修改的投影片後
覺得自己有點弱了
蓮老師都那麼認真的再作投影片,我怎麼能鬆懈呢?
而且又製作動畫,加上所有的圖都自己重新再畫。
我最近也開始要報告了,我看到我學長他們做的投影片
和老師做的投影片,比較起來,真的可以看的出來有沒有用心在報告
後來我做投影片開始把圖重新畫,加上動畫
一篇論文有很多東西,在三小時內,我應該要報告哪些東西,
我覺得這是一件困難的事情,是我還需要去學習的。
week12 : PPT Design (Part 1)
這禮拜老師要我們把論文製作成PPT
老師把高年級的與低年級的分開,來比較投影片的製作
我負責的是最後一段 Conclusion
我的投影片放在: wehd.mcu.edu.tw
分享名稱為: IMH Class
今天上課很開心,還有拍照。
不過Conclusion對我來說,算是比較簡單。
難報告的都讓其他人挑走了。
老師把高年級的與低年級的分開,來比較投影片的製作
我負責的是最後一段 Conclusion
我的投影片放在: wehd.mcu.edu.tw
分享名稱為: IMH Class
今天上課很開心,還有拍照。
不過Conclusion對我來說,算是比較簡單。
難報告的都讓其他人挑走了。
Week 2 : Introduce to Steganography Tool : S-Tools
本文主要是介紹藏匿工具中的一套軟體: S-Tools 的操作。
S-Tools 的 S 所代表的英文單字是Steganography(藏匿)的意思。
目前市面上有很多的藏匿工具。S-Tools 可以將訊息嵌入到 GIF格式 的影像中。
本文的用意在於簡單描述其中一套藏匿工具 S-Tools 的操作。(請按此下載 S-Tools )
請按此下載 S-Tools 的使用說明檔案。
S-Tools 的 S 所代表的英文單字是Steganography(藏匿)的意思。
目前市面上有很多的藏匿工具。S-Tools 可以將訊息嵌入到 GIF格式 的影像中。
本文的用意在於簡單描述其中一套藏匿工具 S-Tools 的操作。(請按此下載 S-Tools )
請按此下載 S-Tools 的使用說明檔案。
Week1 : Introduction to Information Hiding
隨著網路網路(Internet)的蓬勃發展,人們開始藉由網路隨送資料或檔案,但是這樣的一個網路機制,必須要建立在一個具有安全性(Security)的網路上面。試想,若網路傳輸少了安全性,還剩下些什麼 ? 當甲方傳送明文(Plain Text)給乙方時,甲方無法確認該資料是否真的由乙方傳送 ? 在這傳送的過程中,資料是否還完整 ? 資料在傳送途中,如何保證不受到第三者的竊聽與竄改 ?
為了確保明文在傳送過程中,不被第三者竊聽與竄改,於是人們運用密碼學(Cryptography)對明文加密(Encryption),使之變成密文(Cipher Text),通常使明文變的不可讀(non-readable),故此倘若第三者從網路上竊取了傳送端(Sender)所傳送的資料,也無法得知內容。對於情報工作者而言,保密情報是一件非常重要的事情。密碼學Cryptography這單字中,Crypto- 是指secret 的意思,而graph有writing的意思。
在1996年前,相較於密碼學,藏匿學(Steganography)的技術始終受到業界(Industry)及學界(Research Community)比較少的關注。然而隨著多媒體(Multimedia)技術的發展,人們可以輕易的複製這些數位媒體(Digital Media),例如:文字檔(Text)、圖形(Image)、聲音(Audio)、視訊(Video)等,而造成了版權上的問題。由於數位媒體有完整複製(Perfect Copy)的特性,使得不肖業者,可能會未經版權所有者的認可,大量複製(Large-scale Unauthorized Copy)這些數位媒體。對於創作者或版權所有者造成莫大的影響。於是有人想出,把關於著作權的資訊,內嵌(Embedding)於這些數位媒體當中。當數位媒體被複製時,內嵌的著作權資訊也一併被複製了,便於作者對於著作權的追溯。
這和多媒體的進步,有很大的關係。就拿聲音來說好了,過去傳統的聲音是紀錄於錄音帶(tape)中,只能用錄音的方式來複製,而這樣的複製,將會使複製出來的音質產生誤差。換言之,若複製過後的錄音帶,再經過一次複製,將會使複製出來的音質產生更大的誤差,造成失真的現象。而現在儲存音樂大部分是採用數位形式(Digital Form)來儲存,例如:CD(Compact Disc)。當我們燒錄CD或DVD、VCD時,都能夠完整燒錄,並且不失真。
將資訊隱藏(Information Hiding)的這個想法,並非是近代科學才有,而是從以前就有人這樣作了。例如在兩千多年前的古希臘時代,就有人刮除平時書寫用的小臘版,將信息刻在木板上,再重新用蠟封起來,順利通過邊境檢查,送至斯巴達王后手中,王后將蠟除去後,得知戰爭即將來臨的訊息。而在中國也有類似的觀念,例如江南四大才子之一的唐伯虎,在他的著作 – 西江月中,以每個詩句的字首暗喻進入華府為奴僕是為了秋香。
唐伯虎‧西江月
我聞西方大士,為人了卻凡心。秋來明月照蓬門,香滿禪房出徑。
屈指靈山會後,居然紫竹成林。童男童女拜觀音,僕僕何嫌榮頓。
內嵌:〔我為秋香屈居童僕。〕
這樣的著作,在中國稱為內嵌詩,也有著資訊隱藏的概念。可見資訊隱藏除了要隱藏的資訊外,還需要隱藏的媒體,這樣的媒體我們稱為掩護媒體(Cover Media),掩護媒體經嵌入資訊後變成一份偽裝媒體 (stego-media)。若我們仔細看Steganography這個單字,Stegano- 有掩護遮蔽的意思,而則有graph有writing的意思,最早可追溯到古希臘時代。
然而大部分的人對於密碼學和藏匿學容易感到混淆。密碼學主要是在探討將如何將明文經過加密演算法後變為密文,而這個密文要讓除了傳送端與接收端以外的第三者無法推敲出原來的明文。希望明文經過加密後,越讓人經由密文猜測出原來的明文。而藏匿學則是藉由掩護媒體,將需要藏匿的資訊隱藏在媒體中,讓人無法察覺被藏匿的資訊。
舉一個例子來說好了,當甲和乙在網路上進行秘密通訊時,甲將明文加密為密文,之後經由網路傳送給乙。雖然第三者無法得知假傳給了乙什麼樣的訊息,但是藉由亂七八糟的密文可以得知,甲和乙在作秘密通訊。秘密通訊這件事情是容易被察覺的。若甲將密文內嵌於其他媒體上,例如圖片,再經由網路傳送內嵌著資訊的圖片給乙,第三者可以得知甲乙在作通訊,但是第三者會認為,這只是普通的圖片傳輸,沒有什麼秘密通訊的成分在裡面。
相較於直接加密,資訊隱藏的方法更具有保密的作用。將欲保密的資料先經過加密的動作,再隱藏於掩護媒體中,則保密效果更好,如同上了兩層鎖的保險櫃一樣。
在2001年的911事件之前,有人謠傳賓拉登和其他恐怖份子,利用資訊隱藏軟體隱藏恐怖活動的訊息。他們在網路的休閒聊天室,色情佈告欄,其他網站等貼上恐怖攻擊目標的圖片。試想美國的聯邦調查局(FBI)該如何查出這些掩護媒體呢? 張貼的圖片那麼多張,究竟哪一張才是具有嵌入祕密資訊的圖片呢? 還有那麼多人瀏覽過這些圖片,究竟這些瀏覽圖片的人當中,哪些才是賓拉登的黨羽呢? 這是一個難度很高的挑戰。
為了確保明文在傳送過程中,不被第三者竊聽與竄改,於是人們運用密碼學(Cryptography)對明文加密(Encryption),使之變成密文(Cipher Text),通常使明文變的不可讀(non-readable),故此倘若第三者從網路上竊取了傳送端(Sender)所傳送的資料,也無法得知內容。對於情報工作者而言,保密情報是一件非常重要的事情。密碼學Cryptography這單字中,Crypto- 是指secret 的意思,而graph有writing的意思。
在1996年前,相較於密碼學,藏匿學(Steganography)的技術始終受到業界(Industry)及學界(Research Community)比較少的關注。然而隨著多媒體(Multimedia)技術的發展,人們可以輕易的複製這些數位媒體(Digital Media),例如:文字檔(Text)、圖形(Image)、聲音(Audio)、視訊(Video)等,而造成了版權上的問題。由於數位媒體有完整複製(Perfect Copy)的特性,使得不肖業者,可能會未經版權所有者的認可,大量複製(Large-scale Unauthorized Copy)這些數位媒體。對於創作者或版權所有者造成莫大的影響。於是有人想出,把關於著作權的資訊,內嵌(Embedding)於這些數位媒體當中。當數位媒體被複製時,內嵌的著作權資訊也一併被複製了,便於作者對於著作權的追溯。
這和多媒體的進步,有很大的關係。就拿聲音來說好了,過去傳統的聲音是紀錄於錄音帶(tape)中,只能用錄音的方式來複製,而這樣的複製,將會使複製出來的音質產生誤差。換言之,若複製過後的錄音帶,再經過一次複製,將會使複製出來的音質產生更大的誤差,造成失真的現象。而現在儲存音樂大部分是採用數位形式(Digital Form)來儲存,例如:CD(Compact Disc)。當我們燒錄CD或DVD、VCD時,都能夠完整燒錄,並且不失真。
將資訊隱藏(Information Hiding)的這個想法,並非是近代科學才有,而是從以前就有人這樣作了。例如在兩千多年前的古希臘時代,就有人刮除平時書寫用的小臘版,將信息刻在木板上,再重新用蠟封起來,順利通過邊境檢查,送至斯巴達王后手中,王后將蠟除去後,得知戰爭即將來臨的訊息。而在中國也有類似的觀念,例如江南四大才子之一的唐伯虎,在他的著作 – 西江月中,以每個詩句的字首暗喻進入華府為奴僕是為了秋香。
唐伯虎‧西江月
我聞西方大士,為人了卻凡心。秋來明月照蓬門,香滿禪房出徑。
屈指靈山會後,居然紫竹成林。童男童女拜觀音,僕僕何嫌榮頓。
內嵌:〔我為秋香屈居童僕。〕
這樣的著作,在中國稱為內嵌詩,也有著資訊隱藏的概念。可見資訊隱藏除了要隱藏的資訊外,還需要隱藏的媒體,這樣的媒體我們稱為掩護媒體(Cover Media),掩護媒體經嵌入資訊後變成一份偽裝媒體 (stego-media)。若我們仔細看Steganography這個單字,Stegano- 有掩護遮蔽的意思,而則有graph有writing的意思,最早可追溯到古希臘時代。
然而大部分的人對於密碼學和藏匿學容易感到混淆。密碼學主要是在探討將如何將明文經過加密演算法後變為密文,而這個密文要讓除了傳送端與接收端以外的第三者無法推敲出原來的明文。希望明文經過加密後,越讓人經由密文猜測出原來的明文。而藏匿學則是藉由掩護媒體,將需要藏匿的資訊隱藏在媒體中,讓人無法察覺被藏匿的資訊。
舉一個例子來說好了,當甲和乙在網路上進行秘密通訊時,甲將明文加密為密文,之後經由網路傳送給乙。雖然第三者無法得知假傳給了乙什麼樣的訊息,但是藉由亂七八糟的密文可以得知,甲和乙在作秘密通訊。秘密通訊這件事情是容易被察覺的。若甲將密文內嵌於其他媒體上,例如圖片,再經由網路傳送內嵌著資訊的圖片給乙,第三者可以得知甲乙在作通訊,但是第三者會認為,這只是普通的圖片傳輸,沒有什麼秘密通訊的成分在裡面。
相較於直接加密,資訊隱藏的方法更具有保密的作用。將欲保密的資料先經過加密的動作,再隱藏於掩護媒體中,則保密效果更好,如同上了兩層鎖的保險櫃一樣。
在2001年的911事件之前,有人謠傳賓拉登和其他恐怖份子,利用資訊隱藏軟體隱藏恐怖活動的訊息。他們在網路的休閒聊天室,色情佈告欄,其他網站等貼上恐怖攻擊目標的圖片。試想美國的聯邦調查局(FBI)該如何查出這些掩護媒體呢? 張貼的圖片那麼多張,究竟哪一張才是具有嵌入祕密資訊的圖片呢? 還有那麼多人瀏覽過這些圖片,究竟這些瀏覽圖片的人當中,哪些才是賓拉登的黨羽呢? 這是一個難度很高的挑戰。
2007年6月7日 星期四
Week 14 : 上課問題
首先看到這份資料,是網路上的資料,
之前就有看過維紀百科的東西,
中文的發現一大堆東西看不懂,後來比較偏愛英文
關於這份文件,剛看可能不太了解他再說什麼,
有很多的專有名詞,看不懂的比看的懂得多
文章第一段,我提出質疑
文:"PNG 可以被用來無失真地儲存照片,
但是檔案太大,不適合在網頁上放照片"
我記得 PNG,是 Portable Network Graphics
從字面上來推敲,應該是用於網路上的檔案格式
怎麼會說檔案太大,不適合放在網頁上?
之前有看稍微看一下 DCT 的東西,但是還是不了解為何要這樣做。
還有什麼是量化矩陣? 何謂頻率空間?
之前就有看過維紀百科的東西,
中文的發現一大堆東西看不懂,後來比較偏愛英文
關於這份文件,剛看可能不太了解他再說什麼,
有很多的專有名詞,看不懂的比看的懂得多
文章第一段,我提出質疑
文:"PNG 可以被用來無失真地儲存照片,
但是檔案太大,不適合在網頁上放照片"
我記得 PNG,是 Portable Network Graphics
從字面上來推敲,應該是用於網路上的檔案格式
怎麼會說檔案太大,不適合放在網頁上?
之前有看稍微看一下 DCT 的東西,但是還是不了解為何要這樣做。
還有什麼是量化矩陣? 何謂頻率空間?
2007年4月25日 星期三
Week 6: Index Embedded (I)
前言:
LSB的方法,需先將256色調色盤降為32色,
最後的調色盤可被分群為32個group,導致調色盤的不自然,使之容易被破解。
為了改善此缺點,於是有另外一派的研究希望嵌入資訊時,能夠不改變調色盤。
Index Embedded 就是其中一種不更改調色盤的方法。
以下文章描述Index Embedded 的方法,並在結尾提出結論與問題。
以圖一為例(下圖)
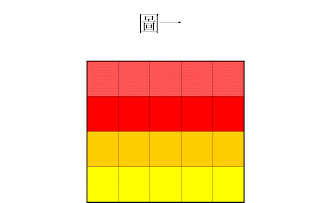
基於 GIF檔 有256種顏色,每張GIF 檔都有一個自己的調色盤。
換言之,不同的圖有不同的調色盤。
首先建立調色盤並且給予相對應的索引值。
第一個顏色給0,第二個顏色給1...依此類推。(圖二)
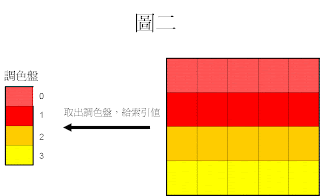
將調色盤,兩兩分組(Pair)。
Index 0 與 Index 1 為一組(Pair)
Index 2 與 Index 3 為一組(Pair)
並將原圖的像素對應到該像素的索引值(Index)(圖三)
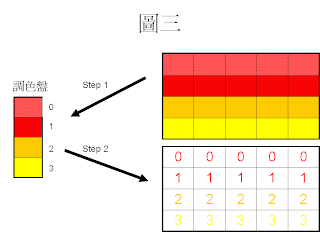
接著嵌入訊息至原圖中:
假若嵌入的資訊為 1010110 1010110
第 1 個bit 1 嵌入第 1 個像素 0(Index值) , 1和0 (Index值)的LSB不相同,
該像素的 index 加1。(找該Index的Pair) 變成 : 0 + 1 = 1(index值為1的顏色)
剩餘嵌入的資訊為 010110 1010110
第 2 個bit 0 嵌入第 2 個像素 0(Index值) , 0和0(Index值)的LSB相同,
該像素的 index 不變。
剩餘嵌入的資訊為 10110 1010110
第 3 個bit 1 嵌入第 3 個像素 0(Index值) , 1和0 (Index值)的LSB不相同,
該像素的 index 加1。變成 : 0 + 1 = 1(index值為1的顏色)
剩餘嵌入的資訊為 0110 1010110
第 4 個bit 0 嵌入第 4 個像素 0(Index值) , 0和0(Index值)的LSB相同,
該像素的 index 不變。
剩餘嵌入的資訊為 110 1010110
第 5 個bit 1 嵌入第 5 個像素 0(Index值) , 1和0 (Index值)的LSB不相同,
該像素的 index 加1。變成 : 0 + 1 = 1(index值為1的顏色)
剩餘嵌入的資訊為 10 1010110
第 6 個bit 1 嵌入第 6 個像素 1(Index值) , 1和1(Index值)的LSB相同,
該像素的 index 不變。
剩餘嵌入的資訊為 0 1010110
第 7 個bit 0 嵌入第 7 個像素 1(Index值) , 0和1(Index值) 的LSB不相同,
該像素的 index 減1。(找該Index的Pair) 變成 : 0 + 1 = 1(index值為1的顏色)
剩餘嵌入的資訊為 1010110
第 8 個bit 1 嵌入第 8 個像素 1(Index值) , 1和1(Index值)的LSB相同,
該像素的 index 不變。
剩餘嵌入的資訊為 010110
第 9 個bit 0 嵌入第 9 個像素 1(Index值) , 0和1(Index值) 的LSB不相同,
該像素的 index 減1。(找該Index的Pair) 變成 : 0 + 1 = 1(index值為1的顏色)
剩餘嵌入的資訊為 10110
第 10 個bit 1 嵌入第 10 個像素 1(Index值) , 1和1(Index值)的LSB相同,
該像素的 index 不變。
剩餘嵌入的資訊為 0110
第 11 個bit 0 嵌入第 11 個像素 2(Index值) , 0 和 2 (Index值)的LSB相同,
該像素的 index 不變。
剩餘嵌入的資訊為 110
第 12 個bit 1 嵌入第 12 個像素 2(Index值) , 1 和 2 (Index值)的LSB不相同,
該像素的 index 加1。(找該Index的Pair)變成 : 2 + 1 = 3(index值為3的顏色)
剩餘嵌入的資訊為 10
第 13 個bit 1 嵌入第 13 個像素 2(Index值) , 1 和 2 (Index值)的LSB不相同,
該像素的 index 加1。(找該Index的Pair)變成 : 2 + 1 = 3(index值為3的顏色)
剩餘嵌入的資訊為 0
第 14 個bit 0 嵌入第 14 個像素 2(Index值) , 0 和 2 (Index值)的LSB相同,
該像素的 index 不變。
PS:上面的步驟是為了目前還不太懂的同學寫的,如果有疑問可以直接找我,
因為我有可能會有筆誤,或是哪裡觀念錯誤,請不吝指正,謝謝。
下圖為原圖與嵌入資訊後的圖片(偽裝媒體)
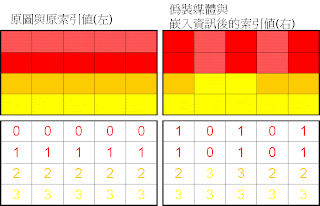
欲取出資訊時,直接取每個像素值的索引值的LSB即可得到隱藏訊息。
<<結論>>
與LSB比較起來,Index Embedded 的方式雖然不改變調色盤,
但是視覺(Visual)上容易察覺圖片可能會是偽裝媒體,
因為造成了顏色不協調的缺點。
在 week 6 看見鄭可欣同學的文章後,立刻與本泰討論顏色不協調的原因,
本泰認為調色盤應該需要經過排序,排序過後應該會使顏色看起來較為協調,
除此之外,Index Embedded 能夠嵌入的資訊量也比 LSB 方法 "少"。
LSB 的方法每個像素可以嵌入3bit,而Index Embedded 每個像素只能嵌入1 bit
除此之外,我提出一個問題是,當原本的圖片並非256色,而是255色時(或更少色時),
原先256色將會有128組pair,但255色將會有127組pair和一個"落單的顏色",
此時應該如何應對?
Week 7 將延續 Week 6 探討改進的方法
LSB的方法,需先將256色調色盤降為32色,
最後的調色盤可被分群為32個group,導致調色盤的不自然,使之容易被破解。
為了改善此缺點,於是有另外一派的研究希望嵌入資訊時,能夠不改變調色盤。
Index Embedded 就是其中一種不更改調色盤的方法。
以下文章描述Index Embedded 的方法,並在結尾提出結論與問題。
以圖一為例(下圖)

基於 GIF檔 有256種顏色,每張GIF 檔都有一個自己的調色盤。
換言之,不同的圖有不同的調色盤。
首先建立調色盤並且給予相對應的索引值。
第一個顏色給0,第二個顏色給1...依此類推。(圖二)

將調色盤,兩兩分組(Pair)。
Index 0 與 Index 1 為一組(Pair)
Index 2 與 Index 3 為一組(Pair)
並將原圖的像素對應到該像素的索引值(Index)(圖三)

接著嵌入訊息至原圖中:
假若嵌入的資訊為 1010110 1010110
第 1 個bit 1 嵌入第 1 個像素 0(Index值) , 1和0 (Index值)的LSB不相同,
該像素的 index 加1。(找該Index的Pair) 變成 : 0 + 1 = 1(index值為1的顏色)
剩餘嵌入的資訊為 010110 1010110
第 2 個bit 0 嵌入第 2 個像素 0(Index值) , 0和0(Index值)的LSB相同,
該像素的 index 不變。
剩餘嵌入的資訊為 10110 1010110
第 3 個bit 1 嵌入第 3 個像素 0(Index值) , 1和0 (Index值)的LSB不相同,
該像素的 index 加1。變成 : 0 + 1 = 1(index值為1的顏色)
剩餘嵌入的資訊為 0110 1010110
第 4 個bit 0 嵌入第 4 個像素 0(Index值) , 0和0(Index值)的LSB相同,
該像素的 index 不變。
剩餘嵌入的資訊為 110 1010110
第 5 個bit 1 嵌入第 5 個像素 0(Index值) , 1和0 (Index值)的LSB不相同,
該像素的 index 加1。變成 : 0 + 1 = 1(index值為1的顏色)
剩餘嵌入的資訊為 10 1010110
第 6 個bit 1 嵌入第 6 個像素 1(Index值) , 1和1(Index值)的LSB相同,
該像素的 index 不變。
剩餘嵌入的資訊為 0 1010110
第 7 個bit 0 嵌入第 7 個像素 1(Index值) , 0和1(Index值) 的LSB不相同,
該像素的 index 減1。(找該Index的Pair) 變成 : 0 + 1 = 1(index值為1的顏色)
剩餘嵌入的資訊為 1010110
第 8 個bit 1 嵌入第 8 個像素 1(Index值) , 1和1(Index值)的LSB相同,
該像素的 index 不變。
剩餘嵌入的資訊為 010110
第 9 個bit 0 嵌入第 9 個像素 1(Index值) , 0和1(Index值) 的LSB不相同,
該像素的 index 減1。(找該Index的Pair) 變成 : 0 + 1 = 1(index值為1的顏色)
剩餘嵌入的資訊為 10110
第 10 個bit 1 嵌入第 10 個像素 1(Index值) , 1和1(Index值)的LSB相同,
該像素的 index 不變。
剩餘嵌入的資訊為 0110
第 11 個bit 0 嵌入第 11 個像素 2(Index值) , 0 和 2 (Index值)的LSB相同,
該像素的 index 不變。
剩餘嵌入的資訊為 110
第 12 個bit 1 嵌入第 12 個像素 2(Index值) , 1 和 2 (Index值)的LSB不相同,
該像素的 index 加1。(找該Index的Pair)變成 : 2 + 1 = 3(index值為3的顏色)
剩餘嵌入的資訊為 10
第 13 個bit 1 嵌入第 13 個像素 2(Index值) , 1 和 2 (Index值)的LSB不相同,
該像素的 index 加1。(找該Index的Pair)變成 : 2 + 1 = 3(index值為3的顏色)
剩餘嵌入的資訊為 0
第 14 個bit 0 嵌入第 14 個像素 2(Index值) , 0 和 2 (Index值)的LSB相同,
該像素的 index 不變。
PS:上面的步驟是為了目前還不太懂的同學寫的,如果有疑問可以直接找我,
因為我有可能會有筆誤,或是哪裡觀念錯誤,請不吝指正,謝謝。
下圖為原圖與嵌入資訊後的圖片(偽裝媒體)

欲取出資訊時,直接取每個像素值的索引值的LSB即可得到隱藏訊息。
<<結論>>
與LSB比較起來,Index Embedded 的方式雖然不改變調色盤,
但是視覺(Visual)上容易察覺圖片可能會是偽裝媒體,
因為造成了顏色不協調的缺點。
在 week 6 看見鄭可欣同學的文章後,立刻與本泰討論顏色不協調的原因,
本泰認為調色盤應該需要經過排序,排序過後應該會使顏色看起來較為協調,
除此之外,Index Embedded 能夠嵌入的資訊量也比 LSB 方法 "少"。
LSB 的方法每個像素可以嵌入3bit,而Index Embedded 每個像素只能嵌入1 bit
除此之外,我提出一個問題是,當原本的圖片並非256色,而是255色時(或更少色時),
原先256色將會有128組pair,但255色將會有127組pair和一個"落單的顏色",
此時應該如何應對?
Week 7 將延續 Week 6 探討改進的方法
Week 8: Index Embedded (III)
在 Week8 的課堂上,我們討論了排序調色盤的方法
本泰用了一種排序方法 r*653356+g*256+b
而老師提供了另外一種以亮度為主的排序方法
但屏除這兩種方式外,老師說還有可以改善的空間。
以我的認知,若是把焦點放在調色盤上,又不希望更動調色盤原來的顏色,
改進的重點應該是調色盤經過大風吹後的新位置。
看了一些同學們作的實驗,不管是以亮度排序或是以r*653356+g*256+b 排序
都沒辦法做到相似的擺在一起。
我認為調色盤的安排,應該要讓越相似的顏色,越放在一起。
而不是用某種鍵值來排序。
應該用分群,而非排序。
讓顏色相似的成群。
而分群的維度,在我的想法中除了算兩個像素(R,G,B)的距離值外
或許可以增加第四個維度"亮度"當作參考維度,即(R,G,B,亮度)。
直覺上應該是用分群,讓顏色相似成群,而非排序。
本泰用了一種排序方法 r*653356+g*256+b
而老師提供了另外一種以亮度為主的排序方法
但屏除這兩種方式外,老師說還有可以改善的空間。
以我的認知,若是把焦點放在調色盤上,又不希望更動調色盤原來的顏色,
改進的重點應該是調色盤經過大風吹後的新位置。
看了一些同學們作的實驗,不管是以亮度排序或是以r*653356+g*256+b 排序
都沒辦法做到相似的擺在一起。
我認為調色盤的安排,應該要讓越相似的顏色,越放在一起。
而不是用某種鍵值來排序。
應該用分群,而非排序。
讓顏色相似的成群。
而分群的維度,在我的想法中除了算兩個像素(R,G,B)的距離值外
或許可以增加第四個維度"亮度"當作參考維度,即(R,G,B,亮度)。
直覺上應該是用分群,讓顏色相似成群,而非排序。
Week 5 : 如何判斷一張雜亂的圖 (續)
Week4 老師提到一個利用機率的方式,
測試一張圖是否為亂亂的圖。
這個方法的中心思想是 "相鄰兩像素間,同色與不同色的比例應相等"
那我根據這個中心思想作下列的實驗:
圖一為一張規律的圖片:黑白相間的圖
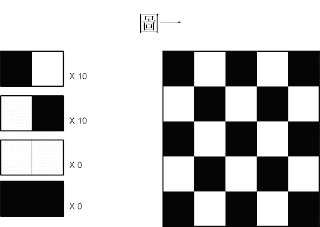
我們首先從圖一開始分析。
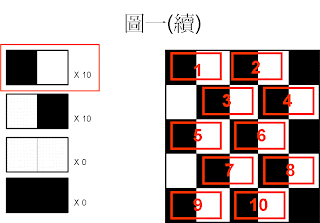
圖一:
黑色右邊是白色佔 10 次,(計算方法請看圖一(續),上圖)
依此類推,白色右邊是黑色佔 10 次,
白色旁邊是白色佔 0 次,黑色旁邊是黑色佔 0 次,
相鄰顏色相同 與 相鄰顏色不同的比例為
(10 + 10) : ( 0 + 0 ) = 20 : 0
比例非常的不均,並非接近1:1,所以認定該圖為一張規律的圖。
接著我們討論圖二(如下):一行黑色一行白色(規律)
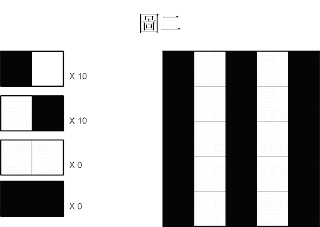
圖二:
黑色右邊是白色佔 10 次,
白色右邊是黑色佔 10 次,
白色旁邊是白色佔 0 次,黑色旁邊是黑色佔 0 次,
相鄰顏色相同 與 相鄰顏色不同的比例為
(10 + 10) : (0+0) = 20 : 0
比例不均,並非接近1:1,認定該圖為一張規律的圖。
接著討論圖三(下圖):左邊是白色,右邊是黑色(規律)
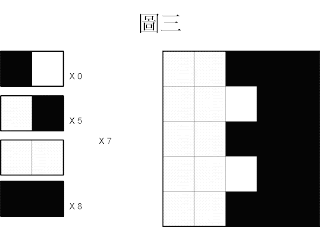
圖三:
黑色右邊是白色佔 0 次,
白色右邊是黑色佔 5 次,
白色旁邊是白色佔 7 次,黑色旁邊是黑色佔 8 次,
相鄰顏色相同 與 相鄰顏色不同的比例為
(0 + 5) : (7+8) = 5 : 15 = 1 : 3
比例不均,並非接近1:1,認定該圖為一張規律的圖。
討論圖四:
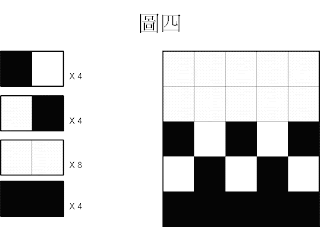
圖四:
黑色右邊是白色佔 4 次,
白色右邊是黑色佔 4 次,
白色旁邊是白色佔 8 次,黑色旁邊是黑色佔 4 次,
相鄰顏色相同 與 相鄰顏色不同的比例為
(4 + 4) : (8+4) = 8 : 12 = 2 : 3
比例不均,並非接近1:1,認定該圖為一張規律的圖。
討論圖五:
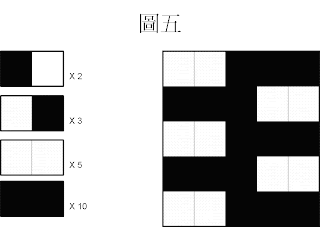
圖五
黑色右邊是白色佔 2 次,
白色右邊是黑色佔 3 次,
白色旁邊是白色佔 5 次,黑色旁邊是黑色佔 10 次,
相鄰顏色相同 與 相鄰顏色不同的比例為
(2 + 3) : 5+10) = 5 : 15 = 1 : 3
比例不均,並非接近1:1,認定該圖為一張規律的圖。
討論圖六:不規律的圖
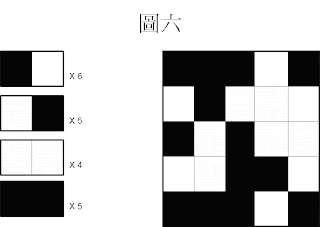
圖一至圖五討論了幾種規律的圖形樣式
圖六討論不規則的圖形樣式
黑色右邊是白色佔 6次,
白色右邊是黑色佔 5 次,
白色旁邊是白色佔 4 次,黑色旁邊是黑色佔 5 次,
相鄰顏色相同 與 相鄰顏色不同的比例為
(6 + 5) : (5+4) = 11 : 9
很接近1:1,認定該圖為一張亂亂的圖。
雖然圖一至圖六,依照此法能夠得判斷該圖是否為雜亂
現在討論圖七(對稱圖形)
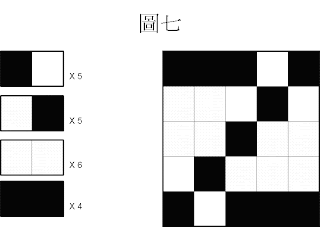
黑色右邊是白色佔 5次,
白色右邊是黑色佔 5 次,
白色旁邊是白色佔 6 次,黑色旁邊是黑色佔 4 次,
相鄰顏色相同 與 相鄰顏色不同的比例為
(5 + 5) : ( 6 + 4 ) = 10 : 10
很接近1:1,依照此法則認定該圖為一張亂亂的圖。
但事實上這張圖我認為是規律的圖,因為這張圖是一張上下對稱的圖形。
結論:
我認為此法無法判斷所有的情況。
測試一張圖是否為亂亂的圖。
這個方法的中心思想是 "相鄰兩像素間,同色與不同色的比例應相等"
那我根據這個中心思想作下列的實驗:
圖一為一張規律的圖片:黑白相間的圖

我們首先從圖一開始分析。

圖一:
黑色右邊是白色佔 10 次,(計算方法請看圖一(續),上圖)
依此類推,白色右邊是黑色佔 10 次,
白色旁邊是白色佔 0 次,黑色旁邊是黑色佔 0 次,
相鄰顏色相同 與 相鄰顏色不同的比例為
(10 + 10) : ( 0 + 0 ) = 20 : 0
比例非常的不均,並非接近1:1,所以認定該圖為一張規律的圖。
接著我們討論圖二(如下):一行黑色一行白色(規律)

圖二:
黑色右邊是白色佔 10 次,
白色右邊是黑色佔 10 次,
白色旁邊是白色佔 0 次,黑色旁邊是黑色佔 0 次,
相鄰顏色相同 與 相鄰顏色不同的比例為
(10 + 10) : (0+0) = 20 : 0
比例不均,並非接近1:1,認定該圖為一張規律的圖。
接著討論圖三(下圖):左邊是白色,右邊是黑色(規律)

圖三:
黑色右邊是白色佔 0 次,
白色右邊是黑色佔 5 次,
白色旁邊是白色佔 7 次,黑色旁邊是黑色佔 8 次,
相鄰顏色相同 與 相鄰顏色不同的比例為
(0 + 5) : (7+8) = 5 : 15 = 1 : 3
比例不均,並非接近1:1,認定該圖為一張規律的圖。
討論圖四:

圖四:
黑色右邊是白色佔 4 次,
白色右邊是黑色佔 4 次,
白色旁邊是白色佔 8 次,黑色旁邊是黑色佔 4 次,
相鄰顏色相同 與 相鄰顏色不同的比例為
(4 + 4) : (8+4) = 8 : 12 = 2 : 3
比例不均,並非接近1:1,認定該圖為一張規律的圖。
討論圖五:

圖五
黑色右邊是白色佔 2 次,
白色右邊是黑色佔 3 次,
白色旁邊是白色佔 5 次,黑色旁邊是黑色佔 10 次,
相鄰顏色相同 與 相鄰顏色不同的比例為
(2 + 3) : 5+10) = 5 : 15 = 1 : 3
比例不均,並非接近1:1,認定該圖為一張規律的圖。
討論圖六:不規律的圖

圖一至圖五討論了幾種規律的圖形樣式
圖六討論不規則的圖形樣式
黑色右邊是白色佔 6次,
白色右邊是黑色佔 5 次,
白色旁邊是白色佔 4 次,黑色旁邊是黑色佔 5 次,
相鄰顏色相同 與 相鄰顏色不同的比例為
(6 + 5) : (5+4) = 11 : 9
很接近1:1,認定該圖為一張亂亂的圖。
雖然圖一至圖六,依照此法能夠得判斷該圖是否為雜亂
現在討論圖七(對稱圖形)

黑色右邊是白色佔 5次,
白色右邊是黑色佔 5 次,
白色旁邊是白色佔 6 次,黑色旁邊是黑色佔 4 次,
相鄰顏色相同 與 相鄰顏色不同的比例為
(5 + 5) : ( 6 + 4 ) = 10 : 10
很接近1:1,依照此法則認定該圖為一張亂亂的圖。
但事實上這張圖我認為是規律的圖,因為這張圖是一張上下對稱的圖形。
結論:
我認為此法無法判斷所有的情況。
2007年3月28日 星期三
Week 4 : 如何判斷一張雜亂的圖
將一張圖的 Last Bit 取出來,形成一個 Bit-Plane,
若這個Bit-Plane是非常雜亂的,
我想這個Bit-Plane 黑點與白點的比例大約是 1 : 1。
如果黑點與白點並非均散於 Bit-Plane 上,
我們會感到某塊區域可能比較黑,或是比較白;
若是均散的狀況下,我們會感到這張圖很雜亂。
假若一張圖的黑白像素比例為 1:1,且黑白像素分散的很平均的狀況下,
我們可以去統計黑白像素點的個數,看看比例是否接近 1:1。
若用這個方法,並不恰當,若一張圖的左半邊全部是黑像素,右半邊全部是白色像素,
雖然統計出來的黑白像素比為 1:1,但是並非均散的狀況。
如下圖 : 此圖只有黑白像素,用0表示白,1 表示黑
ex
0 0 1 1 1
0 0 1 1 1
0 0 0 1 1
0 0 0 1 1
0 0 0 1 1
顯然的,這需要另外的機制來改善這樣的問題。
假若有一張 4x4 的圖片,只有黑白像素,用0表示白,1 表示黑
如下:
1 0 0 1
0 1 0 0
0 1 1 1
1 0 0 1
於此我計算 1 佔了整張圖的比例為 8/16 = 1/2 = 0.5
由我主觀的認為,若一張圖1的數量超過 75%(黑色太多) 或少於 25%(白色太多)
我就認為這張圖不是雜亂的圖。
然後我將這張圖切割數個成 3x3 的小方塊,然後計算該方塊黑色點的比例,
1 0 0 1
0 1 0 0
0 1 1 1
1 0 0 1
方塊 1 ,像素1 的比例為 = 4/9,介於 25% ~ 75% 的臨界範圍內,方塊1 是散亂的
接著看方塊2
1 0 0 1
0 1 0 1
0 1 1 1
1 0 0 1
方塊 2,像素1的比例為 = 6/9 = 0.66,
介於 25% ~ 75% 的臨界範圍內,方塊 散亂的。
接著看方塊3
1 0 0 1
0 1 0 1
0 1 1 1
1 0 0 1
方塊 3,像素1的比例為 = 4/9,介於 25% ~ 75% 的臨界範圍內,方塊3 是散亂的
方塊4
1 0 0 1
0 1 0 1
0 1 1 1
1 0 0 1
方塊 4,像素1的比例為 = 6/9 = 0.66,
介於 25% ~ 75% 的臨界範圍內,方塊4是散亂的。
我們做了四次檢驗,散亂的方塊佔了4 次 = 100%
綜合以上觀點,應該可以斷定這張圖是散亂的。
缺點:
圖片應該選擇怎樣的切割方式,切割大小應該如何選擇會較恰當
臨界值(指75% 與 25%)不易客觀的設定。
PS 以上只是我個人想法,毫無根據。
若這個Bit-Plane是非常雜亂的,
我想這個Bit-Plane 黑點與白點的比例大約是 1 : 1。
如果黑點與白點並非均散於 Bit-Plane 上,
我們會感到某塊區域可能比較黑,或是比較白;
若是均散的狀況下,我們會感到這張圖很雜亂。
假若一張圖的黑白像素比例為 1:1,且黑白像素分散的很平均的狀況下,
我們可以去統計黑白像素點的個數,看看比例是否接近 1:1。
若用這個方法,並不恰當,若一張圖的左半邊全部是黑像素,右半邊全部是白色像素,
雖然統計出來的黑白像素比為 1:1,但是並非均散的狀況。
如下圖 : 此圖只有黑白像素,用0表示白,1 表示黑
ex
0 0 1 1 1
0 0 1 1 1
0 0 0 1 1
0 0 0 1 1
0 0 0 1 1
顯然的,這需要另外的機制來改善這樣的問題。
假若有一張 4x4 的圖片,只有黑白像素,用0表示白,1 表示黑
如下:
1 0 0 1
0 1 0 0
0 1 1 1
1 0 0 1
於此我計算 1 佔了整張圖的比例為 8/16 = 1/2 = 0.5
由我主觀的認為,若一張圖1的數量超過 75%(黑色太多) 或少於 25%(白色太多)
我就認為這張圖不是雜亂的圖。
然後我將這張圖切割數個成 3x3 的小方塊,然後計算該方塊黑色點的比例,
1 0 0 1
0 1 0 0
0 1 1 1
1 0 0 1
方塊 1 ,像素1 的比例為 = 4/9,介於 25% ~ 75% 的臨界範圍內,方塊1 是散亂的
接著看方塊2
1 0 0 1
0 1 0 1
0 1 1 1
1 0 0 1
方塊 2,像素1的比例為 = 6/9 = 0.66,
介於 25% ~ 75% 的臨界範圍內,方塊 散亂的。
接著看方塊3
1 0 0 1
0 1 0 1
0 1 1 1
1 0 0 1
方塊 3,像素1的比例為 = 4/9,介於 25% ~ 75% 的臨界範圍內,方塊3 是散亂的
方塊4
1 0 0 1
0 1 0 1
0 1 1 1
1 0 0 1
方塊 4,像素1的比例為 = 6/9 = 0.66,
介於 25% ~ 75% 的臨界範圍內,方塊4是散亂的。
我們做了四次檢驗,散亂的方塊佔了4 次 = 100%
綜合以上觀點,應該可以斷定這張圖是散亂的。
缺點:
圖片應該選擇怎樣的切割方式,切割大小應該如何選擇會較恰當
臨界值(指75% 與 25%)不易客觀的設定。
PS 以上只是我個人想法,毫無根據。
2007年3月22日 星期四
Week 3 : 想一個破解LSB的方法
Week 3 from 2007/03/15 - 2007/03/21
GIF 屬於調色盤(Palette-based format) 類型的影像資料,支援 256 色。
所謂的256色是指,整張圖片上所有的顏色種類不超過256種顏色。
256 色圖中的每個像素值的範圍都介於 0~255 之間,
256 色圖的像素值,並非代表色彩,而是色彩的編號。
假若一張圖只有 40 種顏色,則在256色圖必須在像素外,紀錄另外一張表格,
這張表格稱為 調色盤 (Palette)。
調色盤上面最多只能紀錄 256 種顏色。
每一張 256 色的圖都有自己的調色盤。
了解了調色盤以後,接著要了解LSB的藏匿方式,
了解了 LSB 後,要破解LSB最直覺的方式,
就是直接把圖片的每個像素中的最後一個位元取出來,
如果取出來後能夠形成一張圖片,或是隱約形成某個圖案,
則說這張圖有藏匿影像。
當然這樣做有它的缺點,
因為機器無法判斷取出來的訊息是有意義的圖片,
圖片也可能藏匿加密過後的影像或是訊息,如果直接取最後一個位元,
取出來仍然看不出來是一張圖片,或是取出看不懂的訊息。
到此,我們了解到,資訊隱藏不一定是藏圖或是文字檔,
有可能是藏匿另外一個已經加密過的資料,這樣的作法讓破解更加的困難。
而取出每個像素的最後一個位元,對於LSB的變形演算法,未必可行,
我所謂的LSB變形的演算法是指,訊息在不一定是隱藏在最後一個位元,
有可能按照別的方式,例如藏在像素的倒數第二個位元,
或是每兩個像素才藏匿一次位元,
或是將原先由左而右藏位元的方式,改成由上而下藏位元。
指由 Row-Major 藏位元的方式改成 Colunm-Major 的方式。
所以這個方法並不是很恰當。
而另外一種方式,檢查偽裝圖片的調色盤,看看是否被分成了32個群。
但是若被嵌入的圖片,原先的色彩就少於32 種顏色,
則無法用這個方式判斷藏匿了資料。
當藏匿的圖片本身顏色數目就很少,資料量不大時,
則看不出來調色盤變成了32 群(小於32群)。
有時候,甚至只是藏匿幾個Bytes的訊息,例如藏匿一句英文。
這種看查看調色盤的方式也會失敗。
GIF 屬於調色盤(Palette-based format) 類型的影像資料,支援 256 色。
所謂的256色是指,整張圖片上所有的顏色種類不超過256種顏色。
256 色圖中的每個像素值的範圍都介於 0~255 之間,
256 色圖的像素值,並非代表色彩,而是色彩的編號。
假若一張圖只有 40 種顏色,則在256色圖必須在像素外,紀錄另外一張表格,
這張表格稱為 調色盤 (Palette)。
調色盤上面最多只能紀錄 256 種顏色。
每一張 256 色的圖都有自己的調色盤。
了解了調色盤以後,接著要了解LSB的藏匿方式,
了解了 LSB 後,要破解LSB最直覺的方式,
就是直接把圖片的每個像素中的最後一個位元取出來,
如果取出來後能夠形成一張圖片,或是隱約形成某個圖案,
則說這張圖有藏匿影像。
當然這樣做有它的缺點,
因為機器無法判斷取出來的訊息是有意義的圖片,
圖片也可能藏匿加密過後的影像或是訊息,如果直接取最後一個位元,
取出來仍然看不出來是一張圖片,或是取出看不懂的訊息。
到此,我們了解到,資訊隱藏不一定是藏圖或是文字檔,
有可能是藏匿另外一個已經加密過的資料,這樣的作法讓破解更加的困難。
而取出每個像素的最後一個位元,對於LSB的變形演算法,未必可行,
我所謂的LSB變形的演算法是指,訊息在不一定是隱藏在最後一個位元,
有可能按照別的方式,例如藏在像素的倒數第二個位元,
或是每兩個像素才藏匿一次位元,
或是將原先由左而右藏位元的方式,改成由上而下藏位元。
指由 Row-Major 藏位元的方式改成 Colunm-Major 的方式。
所以這個方法並不是很恰當。
而另外一種方式,檢查偽裝圖片的調色盤,看看是否被分成了32個群。
但是若被嵌入的圖片,原先的色彩就少於32 種顏色,
則無法用這個方式判斷藏匿了資料。
當藏匿的圖片本身顏色數目就很少,資料量不大時,
則看不出來調色盤變成了32 群(小於32群)。
有時候,甚至只是藏匿幾個Bytes的訊息,例如藏匿一句英文。
這種看查看調色盤的方式也會失敗。
訂閱:
文章 (Atom)