Week 15: JEPG compression (1)

討論的內容包含:
1. 什麼是色彩空間? 為什麼有不同的色彩空間? 轉換的目的為何?
我覺得應該是對於一種色彩的表示方式和計算方法可以視為一個空間,像是線性代數常用的歐式空間等,
色彩的表示方式很多,所以有不同的表示方式,用來加強某些部分的表現程度,所以有不同的色彩空間,
轉換的目的再於讓以某種的表示方式改成另一種,方便日後計算跟表示
2. 什麼是量化? 好處是什麼?
字面上意義應該是說"數量化",很多科學的東西都會提到"量化",像是分等級,用來比較之類的,若是沒有數量化,則很多事情就會變的比較不精確,像是比身高體重等!量化的好處就在於可以讓要描述的東西容易比較,且容易表達
3. 什麼是轉換? 為什麼要做 DCT 轉換?
從一個性質變成另一個性質,為何要做DCT轉換,DCT轉換比較符合自然現象的表現
4. DCT 轉換後的矩陣的意義為何? 何謂低頻? 何謂高頻? 對應到一張影像所呈現的意義是什麼?
低頻:單位時間震動次數較少的波形
高頻:單位時間震動次數較多的波形
代表亮度的頻率

week15 -- (JPEG)

嗯...寫的不多...若寫的有問題...請不吝指教...
1. 什麼是色彩空間? 為什麼有不同的色彩空間? 轉換的目的為何?
由R,G,B或WIKI中提到的YUV都是色彩空間的一種，他們都可以形容色彩，只是組成的基本東西不同，描述顏色的方式不同罷了！
因為每種色彩空間所能夠描述的顏色及方法都不同，每種色彩空間的區域並不會完全一致。
要看需求來選擇轉換色彩空間。
2. 什麼是量化? 好處是什麼?
將複雜的東西轉化為數字，讓我們比較容易了解，並進而使用它。
好處是會使複雜的東西簡單化，變的較好處理。
3. 什麼是轉換? 為什麼要做 DCT 轉換?
嗯...不太會說...
為了要轉換到頻率空間，這樣才可以看的比較清楚，較清楚空間的內容。
4. DCT 轉換後的矩陣的意義為何? 何謂低頻? 何謂高頻? 對應到一張影像所呈現的意義是什麼?
意義...嗯...
頻率：等於週期的倒數，若你做完一個週期的時間長，那麼你的頻率就相對的短(低)，若你花很少時間做完一個週期，那麼頻率就高。
對應後...低頻是相鄰的像素變化率不大，高頻是相鄰的像素變化率大的意思。大約都低頻...畫面是漸漸的、緩慢的變化。

Week15上課筆記

編碼

色彩轉換空間
將影像由RGB轉成YUV(Y：一個像素的亮度，U和V：調色與飽和度)的不同色彩空間，一般的色彩空間由RGB所組成，我們將他轉換成另一種色彩空間YUV，因為人類的眼睛對於亮度看的比調色和飽和度看的更仔細，所以運用YUV的色彩空間讓影像壓縮更有效率
縮減取樣
減少U和V的取樣
離散餘弦變換(DCT)
座標轉換：根據資料特性發展出一套新的座標系統，以減少資料儲存的數量或者是資料比較好被描述
轉換後的座標，左上角就是DC係數(整個亮度的平均值)
量化
將想要表現的東西以數字表現出來
人類對於高頻率的東西，分辨的能力不是很好，所以我們可以運用高頻率降低資訊的數量
轉換後的DCT係數矩陣跟一個量化矩陣作運算，運算後的矩陣會出現蠻明顯的差異

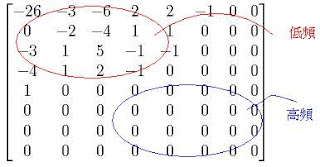
低頻：相鄰兩像素的變化率不大
高頻：相鄰兩像素的變化率大

Week15 JPEG

把老師所提的問題
在經過整理過後
以自己的口吻回答
我覺得我答的不是很好
請大家多多指教
找出我的問題

1. 什麼是色彩空間? 為什麼有不同的色彩空間? 轉換的目的為何?

Ans1:
一群顏色的集合即可稱為色彩空間

Ans2:
不同的色彩空間代表用不同的條件
來形容一群色彩的集合
例如RGB是用紅藍綠三色各佔多少來形容一種顏色
而YCbCr卻是用亮度、色差與飽和度來表達一種顏色
由此可知雖然描述的條件不同卻可同樣用來形容一群顏色

Ans3:
看使用者的需求
像是印表機使用的色彩空間是YMCK
即是一個很好的例子
試想用RGB要怎麼表達出來黑色呢?


2. 什麼是量化? 好處是什麼?

Ans1:
量化即是把一種現象或想描述的事情用數量的形式來表現

Ans2:
可使數據的結果更簡潔
方便觀察或者簡化


3. 什麼是轉換? 為什麼要做 DCT 轉換?

Ans1:
其實轉換的概念我覺得跟色彩空間的轉換概念很像
也是以不同的方式來描述的一群東西的集合
例如要表達平面上的一條線常使用的方法為
y=ax+b
但這個表達是有缺陷的
因為無法表達垂直的角度
因此有人提出了不同的方法
來形容一條線
r = x.cosθ + y.sinθ
這就是一種轉換
而其實這兩個方程式
都是在描述一條線!

Ans2:
因為離散餘弦變換具有很強的"能量集中"特性大多數的自然信號
(包括聲音和圖像)的能量都集中在離散餘弦變換後的低頻部分
所以從講義的8*8陣列可以發現
大部分的頻率都集中到右上角去了


4. DCT 轉換後的矩陣的意義為何? 何謂低頻? 何謂高頻? 對應到一張影像所呈現的意義是什麼?

Ans1:
會有低頻集中在左上角
高頻散佈在右下角的特性

Ans2:

Ans3:

Ans4:

Weak 15 - jpeg

關於jpeg的隱藏技術
由於目前我在做的專研是關於視覺密碼的部份
所以先前也讀了些關於jpeg隱藏浮水印的方法
首先相對於之前的bmp檔案
jpeg檔案是壓縮後的圖像
所以最低位元是壓縮時首先被捨棄掉的部份
(因為最低位元的影像雜亂，捨棄後對原圖沒太大影響)
由於最低位元被捨棄掉了
所以先前所使用的LSB則不適用

再來我要提到空間域及頻率域的技術

空間域:
空間域就是指我們平常圖像用bitmap紀錄的方式
而先前提到的LSB就屬於空間域的技術
但是在jpeg中我們並無法使用LSB來隱藏資訊
因此既然我們無法將資訊隱藏在最低位元中
我們則求其次將資訊隱藏在中頻帶
(由於壓縮影像的資訊隱藏，我們都是先轉至頻率域找出適合隱藏的地方，
然後再轉回空間域，但是在此利用影像四元樹的方法則無須經過此轉換即
可找出中低頻位址，至於頻帶所代表的涵義，我會在頻率域的部份做解釋)
如此一來便能在影響原圖的最低限度下藏入資訊

頻率域:
最簡單的想法，我們將它想成音頻
大概就是長的像那樣的東西
至於我們要如何將空間域的圖片轉換成頻率域
主要是使用以下三種轉換方式:
1.離散餘弦轉換
2.離散小波轉換
3.快速傅立葉轉換
(其轉換公式在此就不詳述，否則真會打不完)
藉由以上方法我們就能將空間域的圖片轉換成頻率域
在頻率域中，我們分成高頻帶、中頻帶、低頻帶三個部份
低頻帶就像是空間域中的最高位元
高頻帶則代表最低位元
由於之前提到最低位元是jpeg影像最優先捨去的部份
所以資訊不能藏在高頻帶
而低頻帶影響圖片最大，所以也不能藏在低頻帶
因此我們所能藏匿的地方就只剩中頻帶了

以上大致就是jpeg這類壓縮圖象隱藏資訊時所用的技術
至於更細節的部分在此也不多詳述

參考論文:
沈伯承-民國92年，中央大學碩士論文，基於灰階視覺密碼之浮水印技術