Week 5 : 如何判斷一張雜亂的圖 (續)

Week4 老師提到一個利用機率的方式，
測試一張圖是否為亂亂的圖。

這個方法的中心思想是 "相鄰兩像素間，同色與不同色的比例應相等"
那我根據這個中心思想作下列的實驗:

圖一為一張規律的圖片:黑白相間的圖


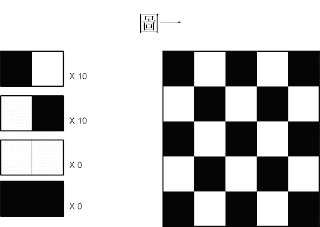
我們首先從圖一開始分析。


圖一:
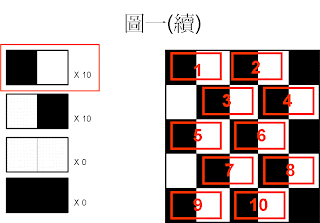
黑色右邊是白色佔 10 次，(計算方法請看圖一(續),上圖)
依此類推，白色右邊是黑色佔 10 次，
白色旁邊是白色佔 0 次，黑色旁邊是黑色佔 0 次，
相鄰顏色相同 與 相鄰顏色不同的比例為
(10 + 10) : ( 0 + 0 ) = 20 : 0
比例非常的不均，並非接近1:1，所以認定該圖為一張規律的圖。

接著我們討論圖二(如下):一行黑色一行白色(規律)



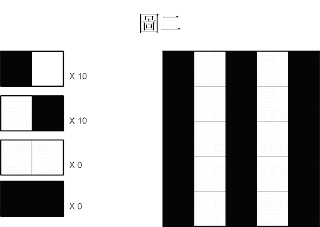
圖二:
黑色右邊是白色佔 10 次，
白色右邊是黑色佔 10 次，
白色旁邊是白色佔 0 次，黑色旁邊是黑色佔 0 次，
相鄰顏色相同 與 相鄰顏色不同的比例為
(10 + 10) : (0+0) = 20 : 0
比例不均，並非接近1:1，認定該圖為一張規律的圖。

接著討論圖三(下圖):左邊是白色，右邊是黑色(規律)


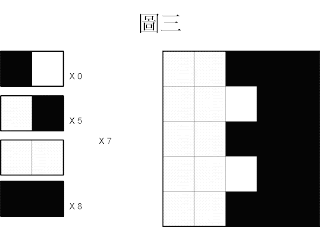
圖三:
黑色右邊是白色佔 0 次，
白色右邊是黑色佔 5 次，
白色旁邊是白色佔 7 次，黑色旁邊是黑色佔 8 次，
相鄰顏色相同 與 相鄰顏色不同的比例為
(0 + 5) : (7+8) = 5 : 15 = 1 : 3
比例不均，並非接近1:1，認定該圖為一張規律的圖。

討論圖四:


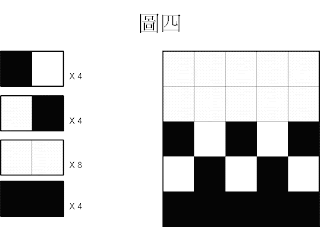
圖四:
黑色右邊是白色佔 4 次，
白色右邊是黑色佔 4 次，
白色旁邊是白色佔 8 次，黑色旁邊是黑色佔 4 次，
相鄰顏色相同 與 相鄰顏色不同的比例為
(4 + 4) : (8+4) = 8 : 12 = 2 : 3
比例不均，並非接近1:1，認定該圖為一張規律的圖。

討論圖五:


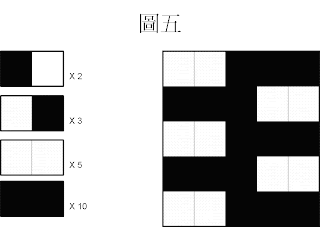
圖五
黑色右邊是白色佔 2 次，
白色右邊是黑色佔 3 次，
白色旁邊是白色佔 5 次，黑色旁邊是黑色佔 10 次，
相鄰顏色相同 與 相鄰顏色不同的比例為
(2 + 3) : 5+10) = 5 : 15 = 1 : 3
比例不均，並非接近1:1，認定該圖為一張規律的圖。

討論圖六:不規律的圖



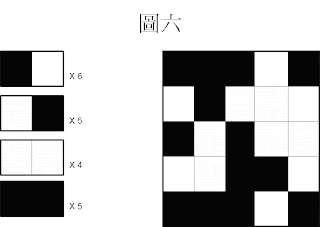
圖一至圖五討論了幾種規律的圖形樣式
圖六討論不規則的圖形樣式
黑色右邊是白色佔 6次，
白色右邊是黑色佔 5 次，
白色旁邊是白色佔 4 次，黑色旁邊是黑色佔 5 次，
相鄰顏色相同 與 相鄰顏色不同的比例為
(6 + 5) : (5+4) = 11 : 9
很接近1:1，認定該圖為一張亂亂的圖。

雖然圖一至圖六，依照此法能夠得判斷該圖是否為雜亂
現在討論圖七(對稱圖形)



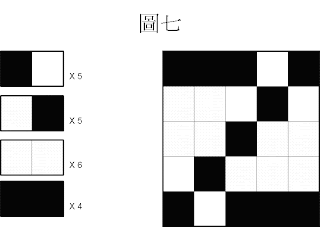
黑色右邊是白色佔 5次，
白色右邊是黑色佔 5 次，
白色旁邊是白色佔 6 次，黑色旁邊是黑色佔 4 次，
相鄰顏色相同 與 相鄰顏色不同的比例為
(5 + 5) : ( 6 + 4 ) = 10 : 10
很接近1:1，依照此法則認定該圖為一張亂亂的圖。
但事實上這張圖我認為是規律的圖，因為這張圖是一張上下對稱的圖形。

結論:
我認為此法無法判斷所有的情況。