計算RMSE(Root Mean Square Error)

上週老師在上課最後提到MSE和PSNR，這兩個都是用來檢測兩張圖是否相似。
MSE的公式為：





PSNR的公式為：





MSE的值愈小，表示兩張圖愈相近。PSNR的愈大，表示兩張圖愈相近。
我試著寫了一個計算MSE和PSNR的小程式，計算方式是先分別將同座標的RGB值相減，
接著將相減後的值平方，累積所有平方後的值，最後累積值除以pixel數便是MSE。
片斷程式碼如下：
r = (point1[x*3+2]-point2[x*3+2])*(point1[x*3+2]-point2[x*3+2]);
g = (point1[x*3+1]-point2[x*3+1])*(point1[x*3+1]-point2[x*3+1]);
b = (point1[x*3]-point2[x*3])*(point1[x*3]-point2[x*3]);
sum = sum+r+g+b;
mse = sum/Hight*Width;
我不太確定這樣計算是否正確，希望其他人可以發表自己查到的結果，供大家討論。
程式執行圖片如下：

Week8

這次延續上週將調色盤排序之後,並將資訊隱藏在圖裡!!!
並且去分析有排序過的和梅排序過的的色差值為多少!!!!

原圖和原圖的調色盤==>
排序過後的調色盤==>
將資訊藏入圖片==>
此圖為未排序過調色盤所藏的圖==>
色差個數比例==>

結果可以看出有排序過的色差各數比例小於沒排序過的!!!!!!

身體狀況不太好
所以好幾週沒去上課了
最近希望能慢慢把進度追上
不過看來只能夠慢慢來了
暫時先慢慢看老師寫的教學日誌來補
可能需要花點時間吧
雖然有點久了，不過上次寫的那個s-tools的檢查工具之前才看到學長說想try看看
那我現在補上，雖然知道有點晚了
http://www.csie.mcu.edu.tw/~s3360256/IH.rar
至於最近在弄的程式，我看先慢慢把進度給追上在說，應該還是來得及
這禮拜只能這樣交代一下了

S-Tool的發現

嗯 感覺這門課很深奧 有種不簡單的感覺 哈
因為基礎不夠深 所以我現階段努力摸索著S-Tool
並且了解圖檔的基本相關資訊等等 如果我自認為有重大發現
而大家覺得沒什麼時......請別笑我 >"< 哈 謝謝 以下就是我所謂測試的重大發現 哈 :p

單看一個圖檔的大小其實是不能判定S-Tool可以將其隱藏滴~ 這該怎說呢?

以下是我的測試：

原始檔資訊：

圖1. JPG 檔

800*600 115KB

圖2. JPG 檔

800*600 129KB

檔名01 使用小畫家轉檔成GIF，檔案大小變成129KB。

檔名02. 使用小畫家轉檔成GIF，檔案大小變成140KB。

可將其隱藏成功！

Memory usage：481,064 bytes

檔名12 使用Photoimpact轉檔成GIF，最佳化128，檔案大小變成146KB。

檔名22 使用Photoimpact轉檔成GIF，最佳化128，檔案大小變成157KB。

可將其隱藏成功！

Memory usage：481,064 bytes

檔名31 使用Photoimpact轉檔成GIF，最佳化256，檔案大小變成184KB。

檔名32 使用Photoimpact轉檔成GIF，最佳化256，檔案大小變成203KB。

↑ 208,741 bytes is too much to fit in here, sorry.

無法隱藏成功！

檔名31小 使用Photoimpact轉檔成GIF，最佳化256，將檔案縮小為400*300，檔案大小變成52.8KB。

檔名32小 使用Photoimpact轉檔成GIF，最佳化256，將檔案縮小為400*300，檔案大小變成57.8KB。

↑ 59,230 bytes is too much to fit in here, sorry.

無法隱藏成功！

結論：

檔案大小並不是影響S-Tool可否隱藏資訊，圖形最佳化是主要影響來源。

◎ 最佳化256，圖檔是400*300，檔案大小是52.8KB，跟最佳化128，圖檔800*600，檔案是146KB，用到的記憶體誰大?

和同學的討論：

開啟時所吃的記憶體是圖越大就越大...400x300大小的全彩圖就是吃400x300x32bit的ram

存在硬碟裡的話，要看壓縮方法...

因為不知道最佳化256跟最佳化128的壓縮比例...所以不知道

但是用相同的壓縮方法的話...一定是圖越大越吃空間

※ 呼呼~ 以上就是我的結論與觀點

不知道是否有誤或不足處，請多指點，謝謝 ^^

Week8:灰階度排序後藏匿的圖

發燒了兩天,今天開始延續上禮拜的動作!
雖然上週回家就完成灰階度的排序!不過這次又再做了另一個小test不過應該是方法用錯吧!
先談談上次用的方法:
也就是灰階的方式排序後的調色盤:

以下是沒排序隱藏資訊的圖:

排序後隱藏資訊的圖:


最後則是謬論做的圖:

本想做成分群的效果,或許理論上可以讓加密的圖更清楚

.首先先從老師的blog下載S-Tools，執行後出現下圖畫面

再來將欲作為分享用圖片自桌面拖曳入S-Tools視窗中，然後如下圖所示 (附註:S-Tools圖片檔只吃.bmp跟.gif這兩種格式，音效檔則只吃.wav格式)

在來將欲隱藏在分享圖片中的資訊自桌面拖曳至分享圖片中，依此步驟執行將會出現如以下圖所示新對話窗要求你輸入加密密碼及隱藏格式

當步驟成立後，如下圖，Actions視窗將會出現正執行之編碼工作

編碼完成將開啟新的視窗，此視窗即為加密後的圖片影像

此時加密後的圖片在外觀上與原分享圖片無異，但在加密後的圖片上點右鍵在點取Rveal的選項會出現以下對話窗，此對話窗則是用來解密加密文件中的訊息所用，此時如果沒有正確的密碼或格式的話，將無法得到加密於其中的文件

如果解密正確則出現以下對話視窗，另存新檔後的檔案則為加密於其中的文件

結論:這軟體對於像我這種初學者來說藏文件是很方便沒錯，不過也如老師所說色盤會因為被修改後成為32個組群的色盤，對於竊取者或監視者而言很容易就被發現藏有額外文件的事實

Week 6: Index Embedded (I)

前言:
LSB的方法，需先將256色調色盤降為32色，
最後的調色盤可被分群為32個group，導致調色盤的不自然，使之容易被破解。

為了改善此缺點，於是有另外一派的研究希望嵌入資訊時，能夠不改變調色盤。
Index Embedded 就是其中一種不更改調色盤的方法。

以下文章描述Index Embedded 的方法，並在結尾提出結論與問題。

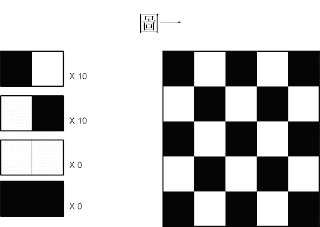
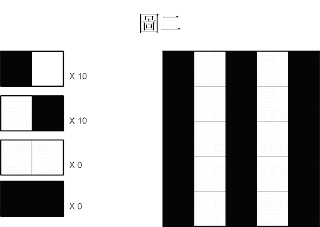
以圖一為例(下圖)



基於 GIF檔 有256種顏色，每張GIF 檔都有一個自己的調色盤。

換言之，不同的圖有不同的調色盤。

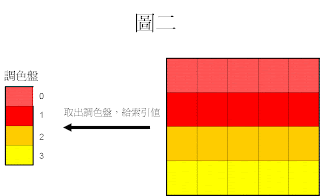
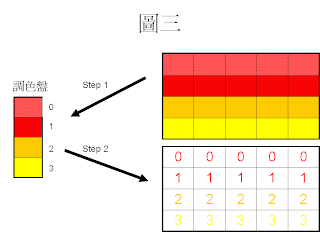
首先建立調色盤並且給予相對應的索引值。
第一個顏色給0，第二個顏色給1...依此類推。(圖二)



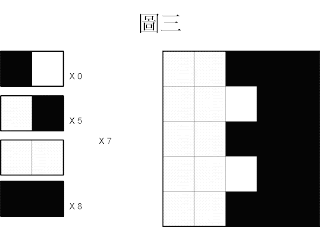
將調色盤，兩兩分組(Pair)。
Index 0 與 Index 1 為一組(Pair)
Index 2 與 Index 3 為一組(Pair)
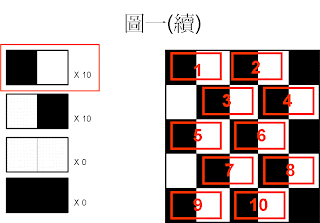
並將原圖的像素對應到該像素的索引值(Index)(圖三)




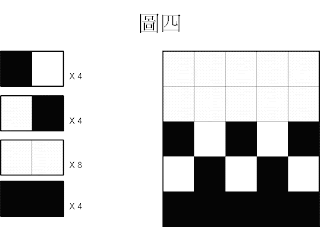
接著嵌入訊息至原圖中:
假若嵌入的資訊為 1010110 1010110
第 1 個bit 1 嵌入第 1 個像素 0(Index值) , 1和0 (Index值)的LSB不相同，
該像素的 index 加1。(找該Index的Pair) 變成 : 0 + 1 = 1(index值為1的顏色)

剩餘嵌入的資訊為 010110 1010110
第 2 個bit 0 嵌入第 2 個像素 0(Index值) , 0和0(Index值)的LSB相同，
該像素的 index 不變。

剩餘嵌入的資訊為 10110 1010110
第 3 個bit 1 嵌入第 3 個像素 0(Index值) , 1和0 (Index值)的LSB不相同，
該像素的 index 加1。變成 : 0 + 1 = 1(index值為1的顏色)

剩餘嵌入的資訊為 0110 1010110
第 4 個bit 0 嵌入第 4 個像素 0(Index值) , 0和0(Index值)的LSB相同，
該像素的 index 不變。

剩餘嵌入的資訊為 110 1010110
第 5 個bit 1 嵌入第 5 個像素 0(Index值) , 1和0 (Index值)的LSB不相同，
該像素的 index 加1。變成 : 0 + 1 = 1(index值為1的顏色)

剩餘嵌入的資訊為 10 1010110
第 6 個bit 1 嵌入第 6 個像素 1(Index值) , 1和1(Index值)的LSB相同，
該像素的 index 不變。

剩餘嵌入的資訊為 0 1010110
第 7 個bit 0 嵌入第 7 個像素 1(Index值) , 0和1(Index值) 的LSB不相同，
該像素的 index 減1。(找該Index的Pair) 變成 : 0 + 1 = 1(index值為1的顏色)

剩餘嵌入的資訊為 1010110
第 8 個bit 1 嵌入第 8 個像素 1(Index值) , 1和1(Index值)的LSB相同，
該像素的 index 不變。

剩餘嵌入的資訊為 010110
第 9 個bit 0 嵌入第 9 個像素 1(Index值) , 0和1(Index值) 的LSB不相同，
該像素的 index 減1。(找該Index的Pair) 變成 : 0 + 1 = 1(index值為1的顏色)

剩餘嵌入的資訊為 10110
第 10 個bit 1 嵌入第 10 個像素 1(Index值) , 1和1(Index值)的LSB相同，
該像素的 index 不變。

剩餘嵌入的資訊為 0110
第 11 個bit 0 嵌入第 11 個像素 2(Index值) , 0 和 2 (Index值)的LSB相同，
該像素的 index 不變。

剩餘嵌入的資訊為 110
第 12 個bit 1 嵌入第 12 個像素 2(Index值) , 1 和 2 (Index值)的LSB不相同，
該像素的 index 加1。(找該Index的Pair)變成 : 2 + 1 = 3(index值為3的顏色)

剩餘嵌入的資訊為 10
第 13 個bit 1 嵌入第 13 個像素 2(Index值) , 1 和 2 (Index值)的LSB不相同，
該像素的 index 加1。(找該Index的Pair)變成 : 2 + 1 = 3(index值為3的顏色)

剩餘嵌入的資訊為 0
第 14 個bit 0 嵌入第 14 個像素 2(Index值) , 0 和 2 (Index值)的LSB相同，
該像素的 index 不變。

PS:上面的步驟是為了目前還不太懂的同學寫的，如果有疑問可以直接找我，
因為我有可能會有筆誤，或是哪裡觀念錯誤，請不吝指正，謝謝。

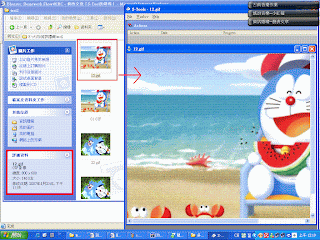
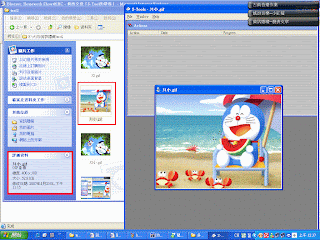
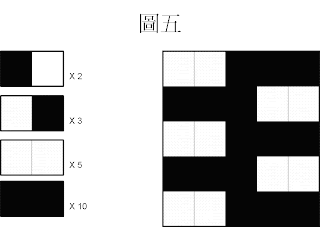
下圖為原圖與嵌入資訊後的圖片(偽裝媒體)



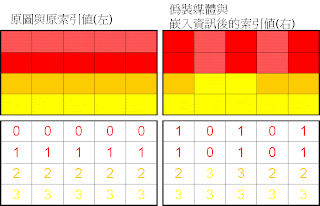
欲取出資訊時，直接取每個像素值的索引值的LSB即可得到隱藏訊息。

<<結論>>

與LSB比較起來，Index Embedded 的方式雖然不改變調色盤，

但是視覺(Visual)上容易察覺圖片可能會是偽裝媒體，

因為造成了顏色不協調的缺點。

在 week 6 看見鄭可欣同學的文章後，立刻與本泰討論顏色不協調的原因，

本泰認為調色盤應該需要經過排序，排序過後應該會使顏色看起來較為協調，

除此之外，Index Embedded 能夠嵌入的資訊量也比 LSB 方法 "少"。

LSB 的方法每個像素可以嵌入3bit，而Index Embedded 每個像素只能嵌入1 bit

除此之外，我提出一個問題是，當原本的圖片並非256色，而是255色時(或更少色時)，

原先256色將會有128組pair，但255色將會有127組pair和一個"落單的顏色"，

此時應該如何應對?

Week 7 將延續 Week 6 探討改進的方法

Week 8: Index Embedded (III)

在 Week8 的課堂上，我們討論了排序調色盤的方法

本泰用了一種排序方法 r*653356+g*256+b

而老師提供了另外一種以亮度為主的排序方法

但屏除這兩種方式外，老師說還有可以改善的空間。

以我的認知，若是把焦點放在調色盤上，又不希望更動調色盤原來的顏色，

改進的重點應該是調色盤經過大風吹後的新位置。

看了一些同學們作的實驗，不管是以亮度排序或是以r*653356+g*256+b 排序

都沒辦法做到相似的擺在一起。

我認為調色盤的安排，應該要讓越相似的顏色，越放在一起。

而不是用某種鍵值來排序。

應該用分群，而非排序。

讓顏色相似的成群。

而分群的維度，在我的想法中除了算兩個像素(R,G,B)的距離值外

或許可以增加第四個維度"亮度"當作參考維度，即(R,G,B,亮度)。

直覺上應該是用分群，讓顏色相似成群，而非排序。

week8筆記

gif檔的調色盤會將所有有用到的顏色放取出來
我們將顏色給一個index的值(gif檔最多只有256色，所以index值最大只到256)
如果我們要隱藏的資訊為010011
我們先取出要隱藏的index(那個index是亂數取嗎???)
例如取出的index為10 18 36 42 60 73
我們將取出的index轉成二進位之後，再將所要隱藏的資訊隱藏在二進位的最後一個數字
index 10 18 36 42 60 73
二進位 1100 10010 100100 101010 111100 1001001
隱藏後的二進位 1100 10011 100100 101010 111101 1001001
index變成10 19 36 42 61 73
將index=18的顏色改成index=19的顏色
將index=60的顏色改成index=61的顏色
如果要將所隱藏的資訊取出來的話，我們必須先知道index的值為多少
但是要如何把index的值讓對方知道又是一個問題
以上此種方法不適合用在bmp檔，因為bmp檔的調色盤沒有限制
如果調色盤被改變，index也會被改變
但是gif檔的調色盤看起來是亂亂的
隱藏後的圖看起來有很大的瑕疵
所以解決方法是將調色盤先依照亮度排序
然後再按照原先的方法進行隱藏
隱藏後的圖看起來就好多了

資訊隱藏(6)

這次討論的是曲線與亮度之間的關析和如何把資料藏在圖中
1.曲線與亮度之間:
當改變曲線時,亮度也會改變,如果曲線是呈現成遞增函數,圖案看起來會較自然,如果取現成歪曲狀,
圖案看起來會較不自然
2.資料藏在圖中
假設我們要把10110101藏在圖的最後一個BIT中,而INDEX值為27.35.60.11.28.90.153.162
那他藏完之後就會變成
一開始的值:027 035 060 011 028 090 153 162
藏完後的職:027 034 061 011 028 091 152 163
預藏的資訊: 1 0 1 1 0 1 0 1

Week 5 : 如何判斷一張雜亂的圖 (續)

Week4 老師提到一個利用機率的方式，
測試一張圖是否為亂亂的圖。

這個方法的中心思想是 "相鄰兩像素間，同色與不同色的比例應相等"
那我根據這個中心思想作下列的實驗:

圖一為一張規律的圖片:黑白相間的圖


我們首先從圖一開始分析。


圖一:
黑色右邊是白色佔 10 次，(計算方法請看圖一(續),上圖)
依此類推，白色右邊是黑色佔 10 次，
白色旁邊是白色佔 0 次，黑色旁邊是黑色佔 0 次，
相鄰顏色相同 與 相鄰顏色不同的比例為
(10 + 10) : ( 0 + 0 ) = 20 : 0
比例非常的不均，並非接近1:1，所以認定該圖為一張規律的圖。

接著我們討論圖二(如下):一行黑色一行白色(規律)



圖二:
黑色右邊是白色佔 10 次，
白色右邊是黑色佔 10 次，
白色旁邊是白色佔 0 次，黑色旁邊是黑色佔 0 次，
相鄰顏色相同 與 相鄰顏色不同的比例為
(10 + 10) : (0+0) = 20 : 0
比例不均，並非接近1:1，認定該圖為一張規律的圖。

接著討論圖三(下圖):左邊是白色，右邊是黑色(規律)


圖三:
黑色右邊是白色佔 0 次，
白色右邊是黑色佔 5 次，
白色旁邊是白色佔 7 次，黑色旁邊是黑色佔 8 次，
相鄰顏色相同 與 相鄰顏色不同的比例為
(0 + 5) : (7+8) = 5 : 15 = 1 : 3
比例不均，並非接近1:1，認定該圖為一張規律的圖。

討論圖四:


圖四:
黑色右邊是白色佔 4 次，
白色右邊是黑色佔 4 次，
白色旁邊是白色佔 8 次，黑色旁邊是黑色佔 4 次，
相鄰顏色相同 與 相鄰顏色不同的比例為
(4 + 4) : (8+4) = 8 : 12 = 2 : 3
比例不均，並非接近1:1，認定該圖為一張規律的圖。

討論圖五:


圖五
黑色右邊是白色佔 2 次，
白色右邊是黑色佔 3 次，
白色旁邊是白色佔 5 次，黑色旁邊是黑色佔 10 次，
相鄰顏色相同 與 相鄰顏色不同的比例為
(2 + 3) : 5+10) = 5 : 15 = 1 : 3
比例不均，並非接近1:1，認定該圖為一張規律的圖。

討論圖六:不規律的圖



圖一至圖五討論了幾種規律的圖形樣式
圖六討論不規則的圖形樣式
黑色右邊是白色佔 6次，
白色右邊是黑色佔 5 次，
白色旁邊是白色佔 4 次，黑色旁邊是黑色佔 5 次，
相鄰顏色相同 與 相鄰顏色不同的比例為
(6 + 5) : (5+4) = 11 : 9
很接近1:1，認定該圖為一張亂亂的圖。

雖然圖一至圖六，依照此法能夠得判斷該圖是否為雜亂
現在討論圖七(對稱圖形)



黑色右邊是白色佔 5次，
白色右邊是黑色佔 5 次，
白色旁邊是白色佔 6 次，黑色旁邊是黑色佔 4 次，
相鄰顏色相同 與 相鄰顏色不同的比例為
(5 + 5) : ( 6 + 4 ) = 10 : 10
很接近1:1，依照此法則認定該圖為一張亂亂的圖。
但事實上這張圖我認為是規律的圖，因為這張圖是一張上下對稱的圖形。

結論:
我認為此法無法判斷所有的情況。

用別人的程式測試...week8

(※)↓以下是錯誤示範↓(※)
(※)↓以下是錯誤示範↓(※)
~~~愛豬意唷~~~
使用陳佳玉同學的程式來用，
放了一些圖片，
(經指證過後發現，
是我沒先將圖存成gif再轉檔bmp導致錯誤)
發現顏色相近，
所做出來的效果，並不是很好...
好像是很不好...下面是原圖

下面是hidden之後，

調色盤沒sort過的圖和調色盤，

下面是hidden之後，
調色盤sort後的圖和調色盤，

(※)↑以上是錯誤示範↑(※)

(※)↑以上是錯誤示範↑(※)

我沒先將圖片存成gif後再轉成bmp檔，

導致我這次實驗的錯誤...Q__Q

Week8 Palette sorting

本週的進度就是延續上週的主題
針對index的部份去作排序
如下圖左邊的調色盤為尚未排序過的
右邊的則是已經排序完成
ex1.1

然後以random的方式產生0或者1去變動index
其判別方法為
if index mod 2 = 0 and random = 1
then index++;
else if index mod 2 = 1 and random = 0
then index=index>>1 ;index= index<<1; else do nothing;
由實驗結果下列圖可知
儘管在排序之後讓整體的品質改善了不少
但色調仍然產生了明顯的變化
也就是說這個方法仍然不夠完美!
ex1.2

ex2.1

ex2.2